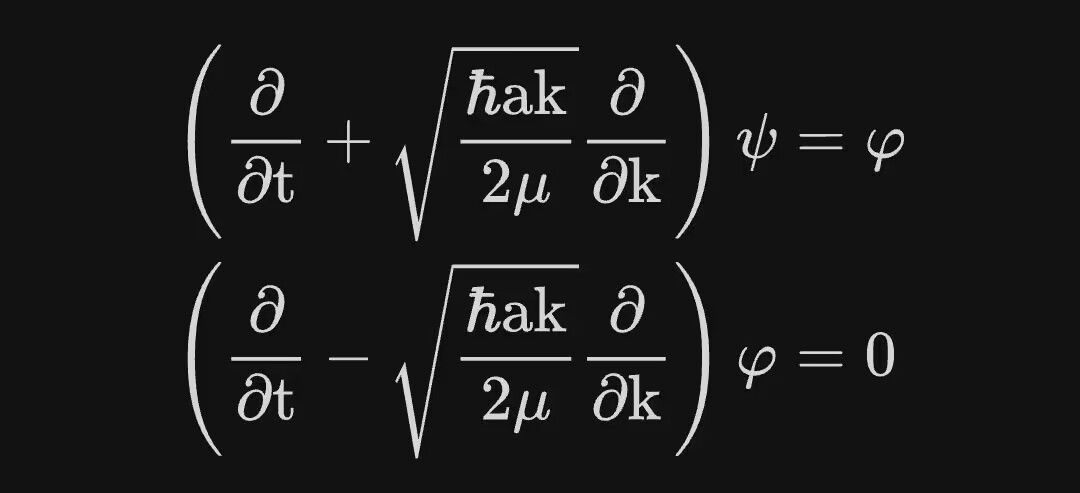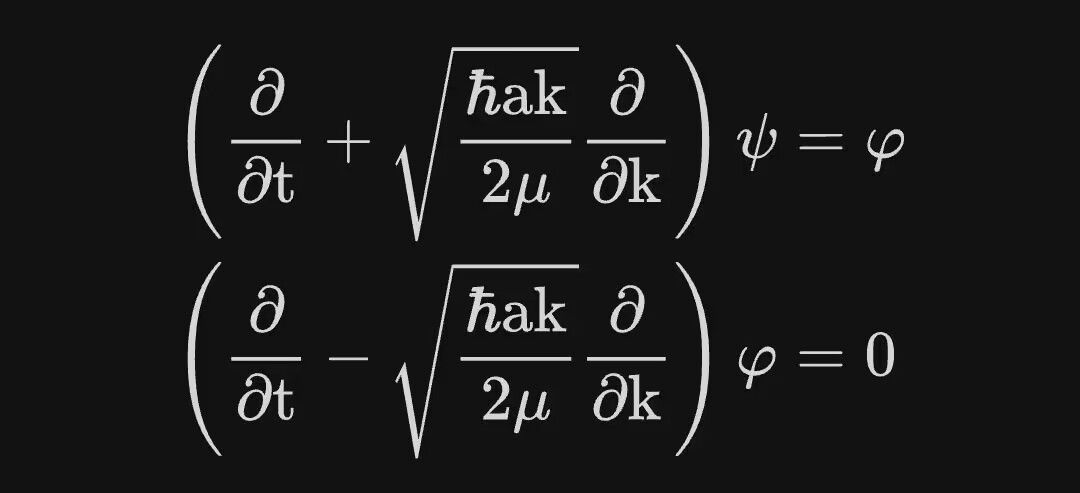案例介绍
通过连续型行波法求解薛定谔方程，得到概率波的解是用从初相相同波矢不同的一系列的行波的叠加，每一列行波的波矢都对应着一个动量，其权重就是相应的概率；也可以从相空间求解，同时得到波矢相同的不同初相的一系列行波的叠加，每一列行波的初相都对应着一个位置，其权重就是该位置的概率。这样分解也反映了粒子在客观上不能同时具有确定的位置和动量。把定态的概率波（驻波）分解为一系列行波，之后对其时频分析，给出从数学与统计学角度构建不确定关系和从平均值算子与对易子构建不确定关系这两种证明方法，体现了对海森堡不确定性关系中“波”的理解。
案例图片
相似案例推荐
其他人才的相似案例推荐
-
中国冰雪
参与了整个项目的分析，数据库设计，负责热图模块、短视频模块(
-
在线答题
编写需求文档，参与部分前端管理员页面的编写 使用Power
-
流量引导
负责测试整个引流过程，过程中涉及H5、小程序、App，多种载
-
上课平台
学生上课应用（涉及多种不同设备和系统：包含MAC、Windo
-
书写四季
项目主要是做书法类的app。面向3岁以上的孩子。 本人主要
-
原初家校通
此项目是一整套校外培训机构管理系统，包括机构管理后台、机构后
-
临池轩
临池轩是一款书法字帖和教学的app，给用户展示名家字帖，临摹
-
美术宝Art-Show
美术宝 art-show 用作学生上传作品展示，老师作品打分
-
Vi跆拳道电子训练设备
该项目主要是用于跆拳道训练比赛中的计分工具，通过得分实时的展
-
自学帮
自学帮是一款提供软件入门课程,办公软件课程,绘画插画课程,动
-
美学权威小程序
美学权威小程序主要以形体仪态为主体的系统，主要针对热爱形态体
-
海丝时尚H5会员系统
海丝时尚H5会员系统是以旗袍为主体衍生的会员系统，主要为旗袍
微信接收人才推送
关注猿急送微信平台，接收实时人才推送
接收人才推送
联系聘用方端客服